力与运动 —— 经典物理大厦
运动的描述
机械运动
如果一个物体相对于另一个物体发生了位置的变化,并且这个变化是由力或能量所驱动的,那么我们可以将其称为机械运动.
形式:平动、转动、振动等.
思考 🤔:位置随时间变化,但是时间是一直在变化的,所以只要发生了空间位置的变化,则为机械运动吗?
回答思考:机械运动通常指的是物体在空间位置上的变化,但并不是所有空间位置的变化都可以归类为机械运动。机械运动通常涉及物体的位移、旋转或震动等,这些变化是由外部力或能量引起的。但是,有些空间位置的变化可能是由其他因素引起的,例如化学反应、热膨胀或量子力学效应等.
此外,机械运动还涉及到物体的力学特性,例如速度、加速度和力等。如果空间位置的变化是由这些力学特性驱动的,那么可以说是机械运动。然而,如果变化是由其他因素引起的,如电磁场的作用或量子态的变化,那么它可能不被称为机械运动.
参考系
用来做参考的一个或者多个具有相同运动状态的物体,称为参照物或者参考系.
参考系选取得当,会使问题的研究更加简洁方便.
被选择为参照物的物体,视为静止,默认以大地为参考系.
- 参照物可以任意选择(_除研究对象外_)
- 默认为大地
- 参照物被视为绝对静止
- 静止是相对的,运动是绝对的!
思考 🤔:如何理解这个具有相同运动状态的物体?
回答思考:具有相同运动状态的物体是指它们在空间中的位置和速度等方面的运动特征是相同的。这意味着它们以相同的速度、方向和加速度等运动,它们之间的相对位置保持不变。
例如,考虑两辆以相同速度和方向行驶的汽车。它们具有相同的运动状态,因为它们以相同的速度和方向移动,彼此之间的相对位置保持不变。
同样地,如果一组物体以相同的速度和方向绕着一个中心旋转,它们也具有相同的运动状态。它们相对于中心点的距离和角速度相同,因此它们的运动状态是相同的.
坐标系
为了定量描述物体的位置及位置变化,要在参考系上建立适当的坐标系.
坐标系三要素:
- 原点
- 正方向
- 单位长度
质点
忽略物体的大小和形状简化成的有质量的点,叫做质点.
- 它是一个理想化模型,现实中不存在!
- 质点当然没有物体本身表达的多,但是它更加直观,方便研究.
根据具体问题来判断是否可以看作质点:
- 在物体体积或者形状不影响问题时可看作质点!
时间和时刻
- 时刻:一个瞬间(点)
- 时间间隔(时间):一段过程,两个时刻之间的时间间隔
例题:

- 第 n 秒内:第 n 个1 秒内
矢量与标量
- 矢量:有大小有方向的物理量
eg:力、位移、面积 - 标量:只有大小的物理量
eg:质量、长度、电荷量、电流、温度 大小比较:
矢量需要规定正方向,在比较时用绝对值来比较
- 3m/s<|-5m/s |
- 3N<|-5N |
标量需要具符号的实际意义而定:
- 3C(库伦)<-5C
- 3℃>-5℃
思考 🤔:
- 为什么电荷量有正负却是标量?
- 为什么电流有方向却是标量?
- 为什么温度有正负却是标量?
- 为什么面积是矢量?
回答思考:
- 电荷量的正负号是用于区分电荷性质的,与方向无关
- 电流的方向是人为定义的,无实际方向
- 温度的正负是以 0 为分界线的数值,与方向无关
- 在《磁场》中,磁感线迎磁场方向不同,效果不同.
路程和位移
- 路程:轨迹的长度.
单位:m、km
标矢:标 - 位移:位置变化
方向:初位置>末位置
单位:m、km
标矢:矢 - 区别和联系:
初末位置相同:

- 路程有多种,位移只有一个!
- _单方向直线运动下_,路程=位移大小(标矢不能直接相同)
- 始终,路程$\ge$位移大小
- 路程是多段位移的积分,位移不一定是路程的微分
速
速度
- 速度:描述运动快慢的物理量,是位移对时间的变化率
- 定义式:$v=\frac{x}{t}$(位移/时间)
- 单位:m/s、km/h
- 标矢:矢
- 方向:和运动方向相同
$\lim\limits{{\Delta t} \to 0} {v=v_{瞬时}}$
$\frac{x}{\Delta t}=\bar v$
速率
- 定义式:$v=\frac{s}{t}$
$\lim\limits{{\Delta t} \to 0} {v=v_{瞬时}}$
加速度
- 加速度:速度变化快慢的物理量
- 定义式:$a=\frac{\Delta v}{\Delta t}=\frac{v_t}{\Delta t}$(比值定义式,_可计算但不取决_)
- 单位:$m/s^2$
- 标矢:矢
- 方向:与$\Delta v$方向相同

- $a、v_0$方向相同,$\Delta v>0$
- $a、v_0$方向相反,$\Delta v<0$
图像
x-t 图像
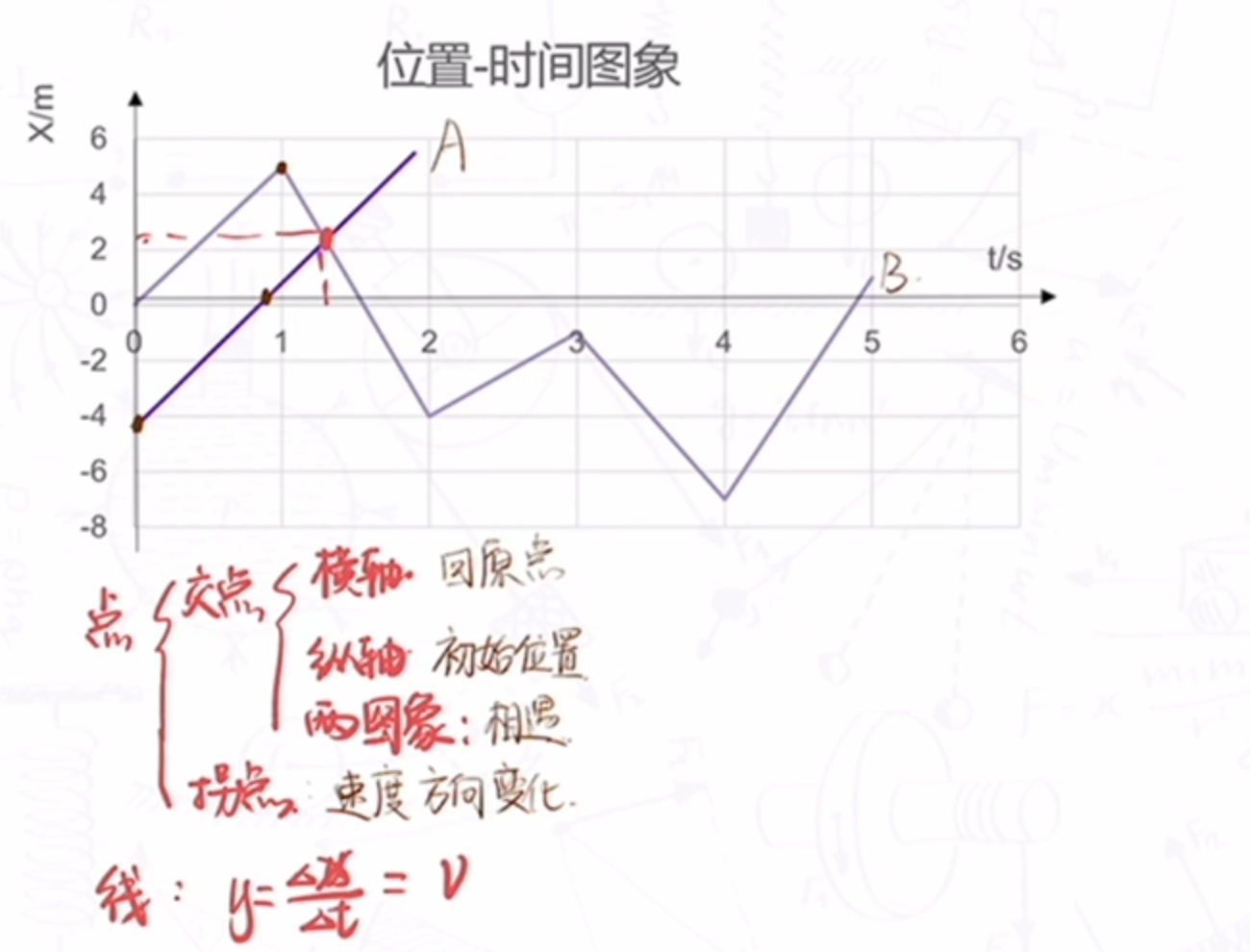
v-t 图像
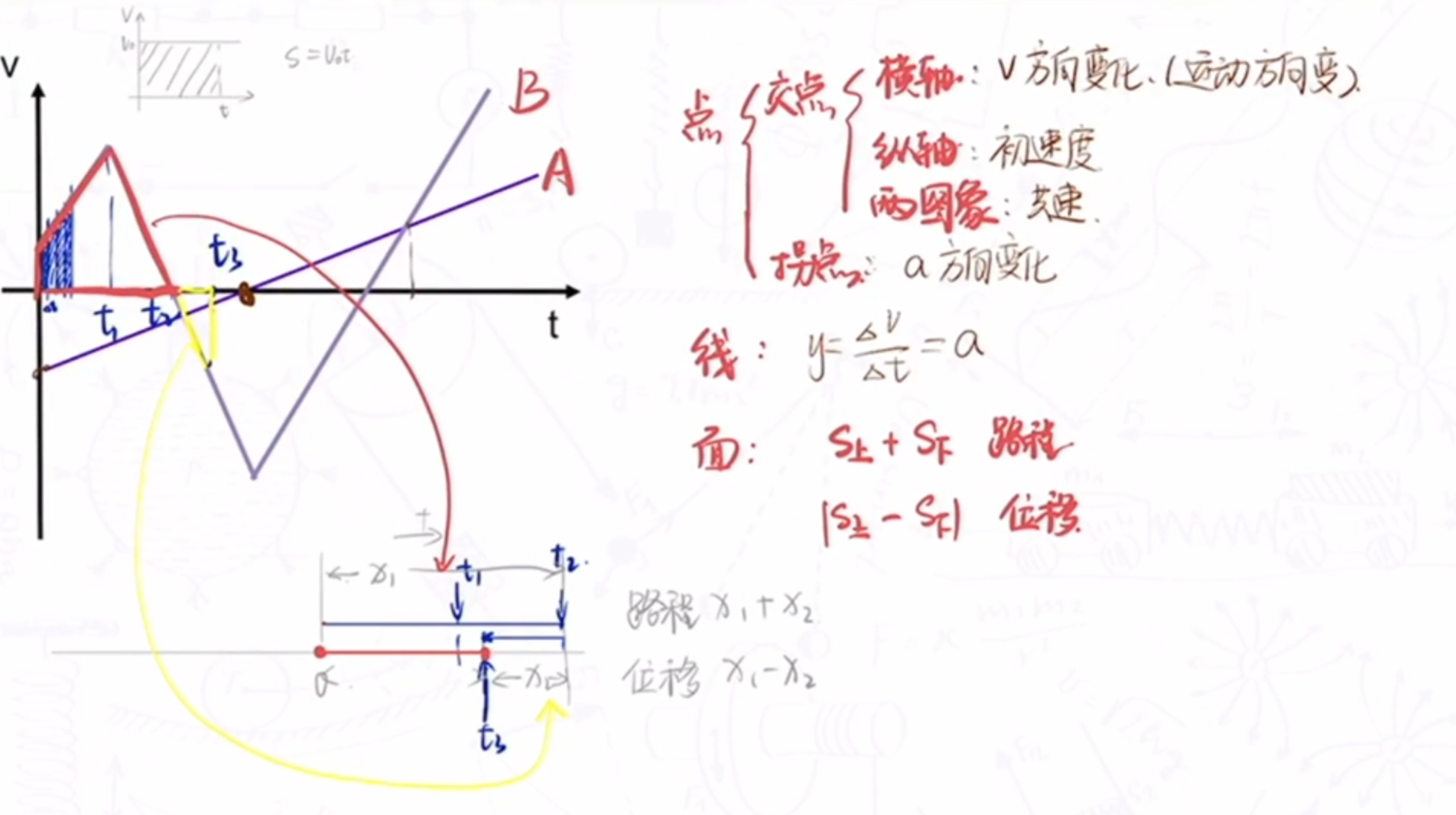
其中,单面积等于单位移是通过微元法推导出的.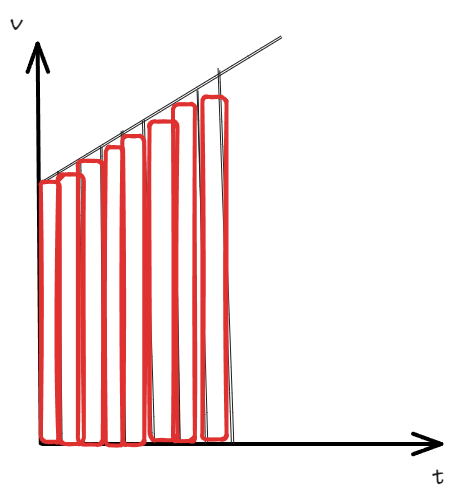
切得越多,上方小三角形越趋近于 0.所以看作无穷小量.
自我思考 🤔:速度和加速度视为物体的性质,但是需要时间的运行携带驱动.这样就很好理解面积即为位移了.
匀变速直线运动
a(加速度)为定值且$\ne0$的运动为匀变速直线运动.
基本公式
- 要素:$v_0、v_t、a、t、x$
- 要熟练掌握三角函数的运算
公式:
- $v_t=v_0+at$
- $x=v_0t+\frac{1}{2}at^2$
- $\bar v=\frac{x}{t}=\frac{v_0+v_t}{2}$(后式只适用于匀变直)
- $2ax={v_t}^2-{v_0}^2$(匀变直)
- $x=\frac{v_t^2}{2a}$($v_0=0$)
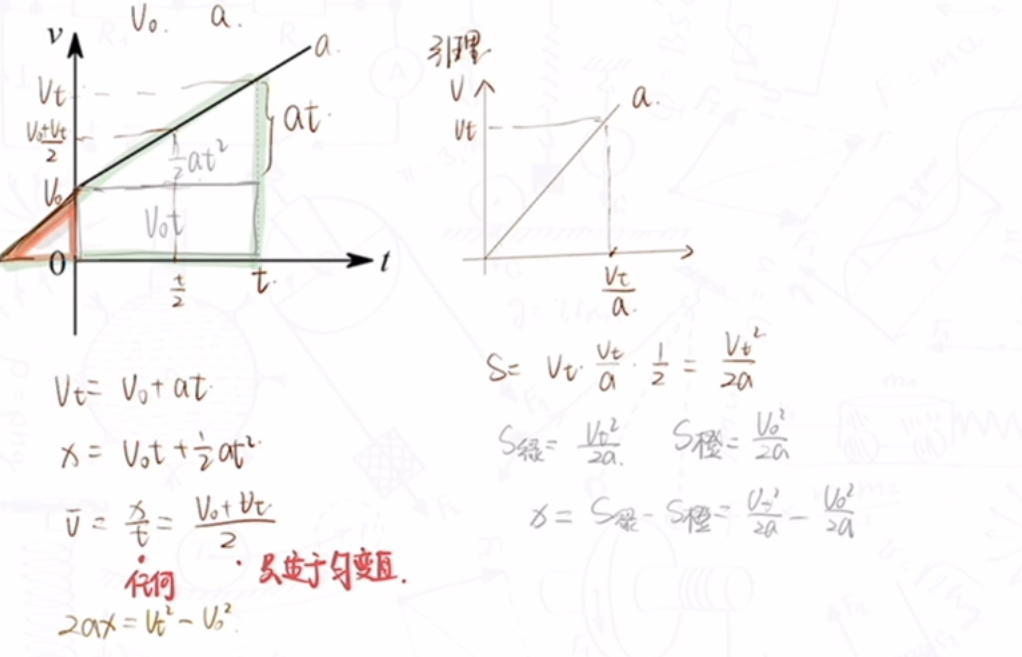
常见推论: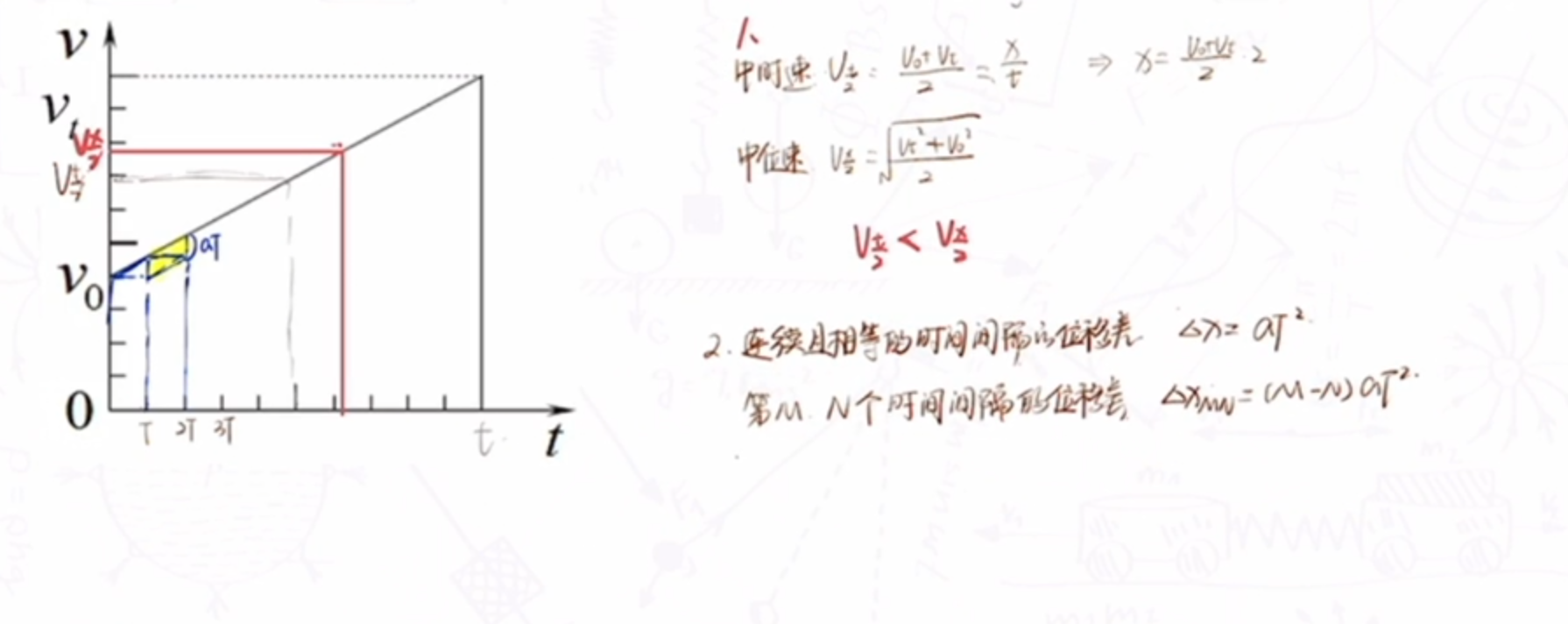
- 能让初速度为零,就尽量.
利用图像来推导十分简单,但是最好自己仔细思考一下为什么.
思考 🤔: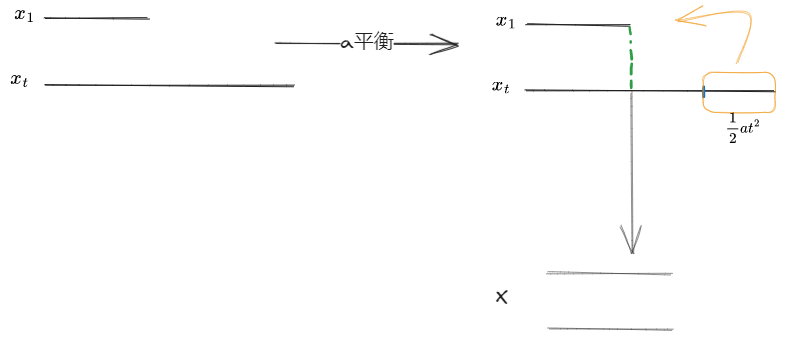
匀变速直线运动进阶
自由落体
- 性质特点:与质量无直接关系,只与重力和空气阻力有关.
- 数据特点: $v_0=0,a=g$
- $v_t=gt,h=\frac{1}{2}gt^2,v_t^2=2gh,\bar v=\frac{v_t}{2}$
一些推论
从零开始的匀变速直中,速度比和时间比相等
使用v-t 图像三角形相似来推.
等时比

等位比

常见力
力的学习路线:
力的命名
- 性质力
以力的性质来命名,例如:
重力、摩擦力 - 效果力
以力的作用效果命名,例如:
拉力、推力、压力
性质力是效果力的因.
范围命名:
- 强力:核子的相互作用力
- 弱力:发生在基本粒子内部的一种作用,使一种粒子衰变成其他的粒子
- 万有引力
- 电磁力:弹力、摩擦力...
重力
- 定义:有地球对物体的吸引而产生的力叫重力.
- 大小:G=mg(g 为重力加速度,取决于高度和纬度)
- 重心:有体积的物体每一份都受重力,而宏观上可以等效为重心受重力.物体重心不一定在物体上,例如:甜甜圈、手镯.
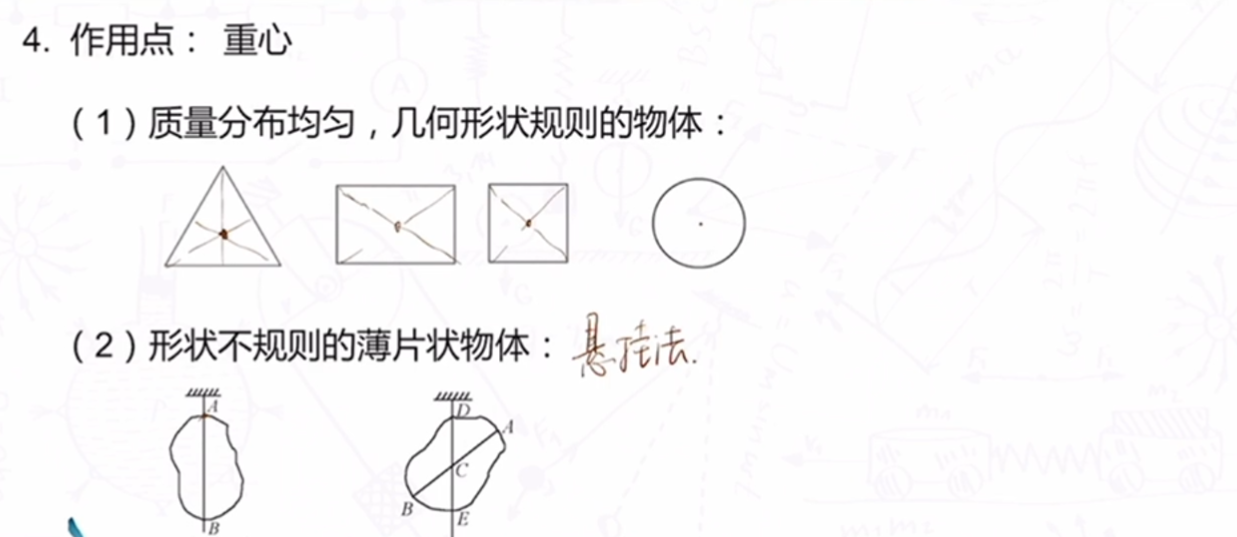
- 方向:竖直向下(或垂直水平向下)
- 注意:因为地球是椭圆的,东西比南北宽,所以重力不是指向地心的,万有引力是指向地形的,所以重力是万有引力的一个分力.
弹力
发生弹性形变的物体,由于要恢复原状,对跟它接触的物体产生力的作用.
画在中心,与其它力成为共点力,方便受力分析.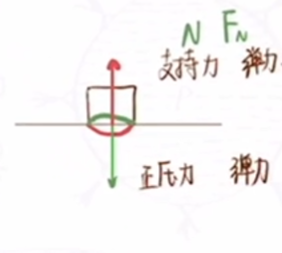
产生条件:
- 接触
- 弹性形变
方向:
- 绳:沿绳收缩的方向,一根绳上的张力大小是相同的(绳上弹力也称张力 )
- 弹簧:沿弹簧指向弹簧原长方向
- 面:有面垂直于面,无面垂直切线
杆:
- 活杆:有脚接.沿杆方向(内外自己分析).
- 死杆:无脚接.方向不一定,结合运动状态分析.

- 活杆:有脚接.沿杆方向(内外自己分析).
大小:
不明显的弹力计算:
- 物体匀速/静止:$F_合$=0
- 物体有加速度:$F_合$=ma
弹簧中弹力:在弹性限度内,弹力大小总是与弹簧的型变量大小正比
- $F=k\Delta x$
- k:劲度系数,取决于弹簧本身材料.单位:N/m
- $\Delta x$:形变量.$\Delta x=|l_1-L_0|$.
- 两侧施力=一侧施力:可以把弹簧想象为只有一侧可以拉动,而弹力是维持原样的力,所以需要克服这个一侧的力.
- 杆的受力可以使用正交分解定量分析.
摩擦力
- 定义:两个相互接触挤压的物体,当他们发生相对运动或具有相对运动的趋势时,就会在接触面上产生阻碍相对运动或相对运动趋势的力.
产生条件:
- 接触并挤压
- 接触面粗糙
- 发生相对运动或具有相对运动趋势.
- 方向:

分类
- 静摩擦
- 滑动摩擦
- 滚动摩擦
滑动摩擦
产生条件:
- 接触并挤压
- 接触面粗糙
- 相对运动
方向:与相对运动方向相反.
- 努力让两个物体共速的力
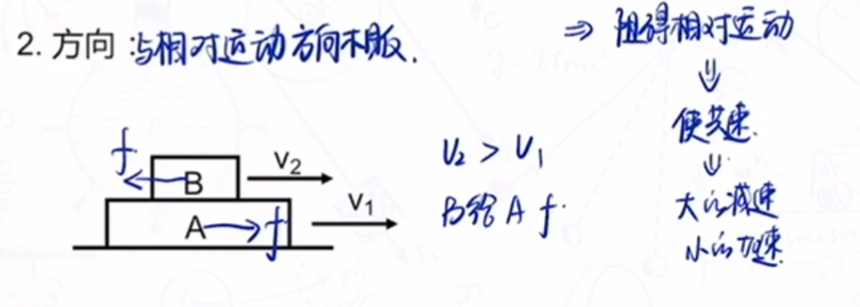
- 努力让两个物体共速的力
大小:
- $f=muF_N$.
- $\mu$:接触面的动摩擦因数,正常情况下<1.
- $F_N$:正压力.
静摩擦力
产生条件
- 接触并挤压
- 接触面粗糙
- 相对运动趋势
方向:
- 与相对运动趋势相反.
- 与之平衡力的等大反向.
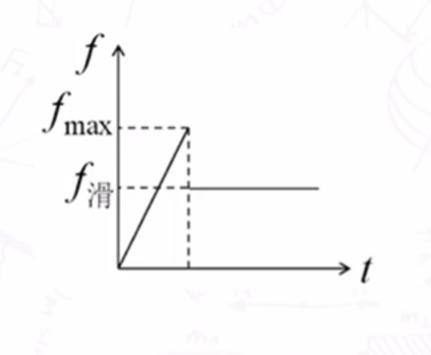
大小:
- 取值范围:$0<f\le f_{max}$.
- 最大静摩擦力 1. 静摩擦力能取到的最大值. 2. 只与压力和接触面的摩擦系数有关. 3. 略大于滑动摩擦力,通常认为$f_滑=f_{max}$
力的合成与分解
合力与分力
当一个物体受到几个力的共同作用时,这个力产生的作用效果跟原来几个力的共同效果相同,这个力叫做那几个力的合力,原来那几个力叫做分力
只是作用效果上的等效替代,不是实际受到的力.只是便于分析而已.
力的合成
- 定义:求几个共点力的合力叫做力的合成.
合成法则:
平行四边形定则.
- 将要合成的 2 个力变成共点力.
- 以这两个力为邻边,做平行四边形.
- 共点的对角线就是合力.
- 使用余弦定理求值($0^\circ < \theta \leq 180^\circ$):
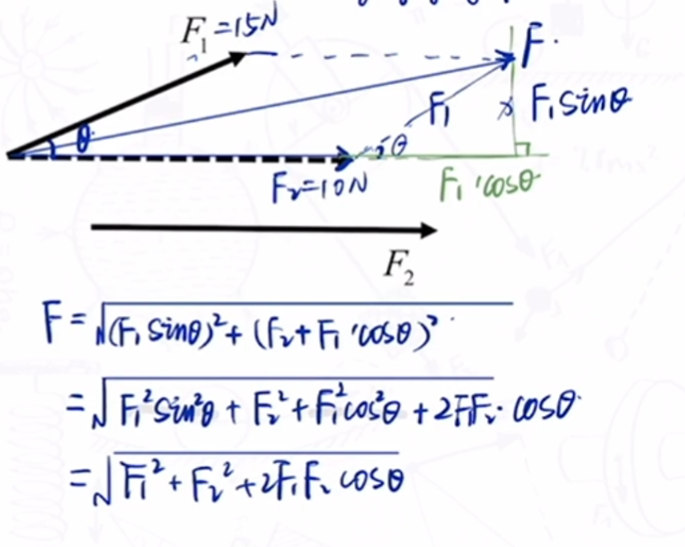
- cos 函数图象:
当$\theta=0$时,$F=F_1+F_2$
当$\theta=180$时,$|F=F_1-F_2|$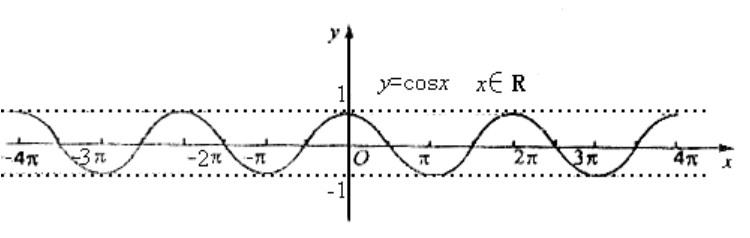
特殊角度:
- 当$\theta=120 ^\circ、F_1=F_2$时,$F_合=F_1=F_2$.
- 当$\theta=60 ^\circ、F_1=F_2$时,$F_合=\sqrt 3 F_1=\sqrt 3 F_2$
三角形定则:
- 平移任意力使首尾相连
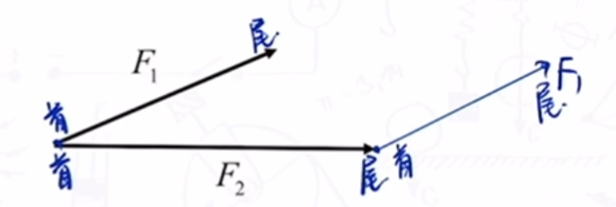
- 矢量 1 头指向矢量 2 的尾即为合力. 矢量 1:未平移的力
- 平移任意力使首尾相连
三力合成:
合成方法:
- _两两合成.顺序随意_.
- 将合成的两个分力视作一个合力.
- 合成合力 1 和分力 3.
特殊:
- 如果多个力能够平移到首尾相连构成封闭图形,则合力为 0.

- 物体在几个力的作用下,合力为 0,则其中任意一个力与其他力的合力等大反向.
- 如果多个力能够平移到首尾相连构成封闭图形,则合力为 0.
力的分解
- 定义:求一个已知力的分力
力的分解时力的合成的逆运算.同样遵循力的合成的法则. - 方法:以要分解的力为对角线,选定分解方向做出平行四边形,那么邻边就代表了分力.
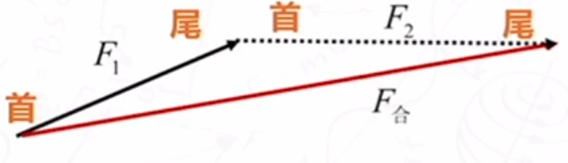
多解——力的分解
力的分解的几种情况:
- 已知合力的大小方向和一个分力的大小方向,另一个分力有几种可能?
一种可能.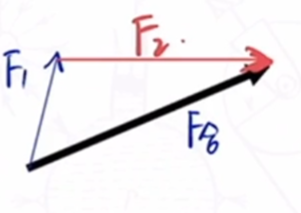
- 已知合力的大小方向,两个分力的方向,两分力有几种可能?
一种可能.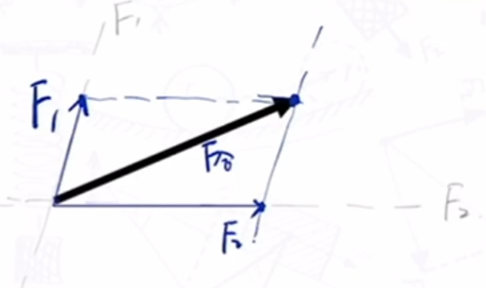
- 已知合力的大小方向,两个分力的大小,两个分力有几种可能?
2 种、或 1 种可能. 或两圆相切. 4. 已知合力大小方向,一个分力的方向,另一个分力大小时,有几种情况?
或两圆相切. 4. 已知合力大小方向,一个分力的方向,另一个分力大小时,有几种情况?
两种或一种情况.
或相交 1. 相切时:$F_2=F_合\cdot sin\theta$. 2. 相交时:$F_2>F_合\cdot sin\theta$.
- 已知合力的大小方向和一个分力的大小方向,另一个分力有几种可能?
正交分解
把力沿着两个选定的互相垂直的方向分解,叫做力的正交分解.
ps:匀速和静止时,合外力为 0.
步骤:
- 选取研究对象:
可以是单个物体,也可以是多个物体组成的系统 - 受力分析:
注意分析顺序:一重二外三弹四摩擦 - 建立直角坐标系:
沿 v/a 方向建立 x 轴,沿垂直方向建 y 轴.
应吧所有力平移的共起点,在以该点为坐标原点建系. - 把不在轴上的力向双轴投影
- 根据运动状态,分别对两轴列方程
- 代数计算
- 选取研究对象:
力学问题综合
平衡状态
合外力为零就平衡.状态有: 1. 静止 2. 缓慢移动 3. 匀速直线运动
判断:
- 二力:等大、反向、共线
- 三力(不共线):矢量图为闭合三角形
- 多力:任一个力与其它力的合力等大反向共线.
- 正交分解,坐标轴上的合力为 0
多物体解决方法
整体法:
- 前提:物体加速度相同.
- 提示:研究非内力,当物体个数$\ge2$时可以考虑.
隔离法:
- 研究内力.
动态分析
共点力作用下物体平衡的动态分析.
表达式法
- 使用条件:物体受力多于或等于 3 个.
操作步骤:
- 对物体进行受力分析,正交分解后列出两个方向上的平衡方程
- 通过推导待求力的表达式判断力的大小变化
矢量三角形法(动态三角形)
使用前提:1 恒力+1 转力+1 不转力
- 有一个不变量,如重力
- 还有一个方向不变的力
操作步骤:
- 固定恒力
- 平移方向不变力
- 转动未知力
相似三角形
适用条件:
- 矢量三角形与总体图像长度有相似关系
操作步骤:
- 画出矢量三角形
- 将矢量三角形和相似三角形做比
- 结合相似三角形各边长度变化关系判断.
快乐三角形
- 适用条件:1 恒力+2 夹角不变的转力
操作步骤:
- 将力平移到同一矢量三角形中
- 找到不变力与不变角
- 判断对应边的变化.
牛顿运动定律
牛顿第一定律
- 内容:一切物体总是保持静止或匀速直线运动状态,直到有外力迫使它改变这种状态为止.
理解:
- 牛一指出了物体不受力时的运动规律
- 牛一揭示了:_力是改变物体运动状态的原因_,而不是维持物体运动状态的原因
- 不能用实验直接证明.
惯性
- 概念
物体保持原有静止状态或匀速直线运动状态的性质 特点
- 普遍性:一切物体均有惯性
- 无关性:与运动状态无关,与是否受力无关
- 唯一性:只由质量决定,质量越大,惯性越大
- 惯性不是力,物体受到惯性力的说法错误.
牛顿第三定律
- 内容:两个物体之间的作用力与反作用力总是大小相等,方向相反,作用在同一条直线上.
- 应用:划船、跑步、游泳、汽车行驶、喷气飞机
- 判断标准:互为施力物体.
牛顿第二定律
- 内容:物体加速度大小跟物体所受的合外力成正比,跟物体质量成反比,加速度的方向跟合外力的方向相同.
- 表达式:
$a=\frac{F_合}{m}$——决定式 - 性质:

力学单位制
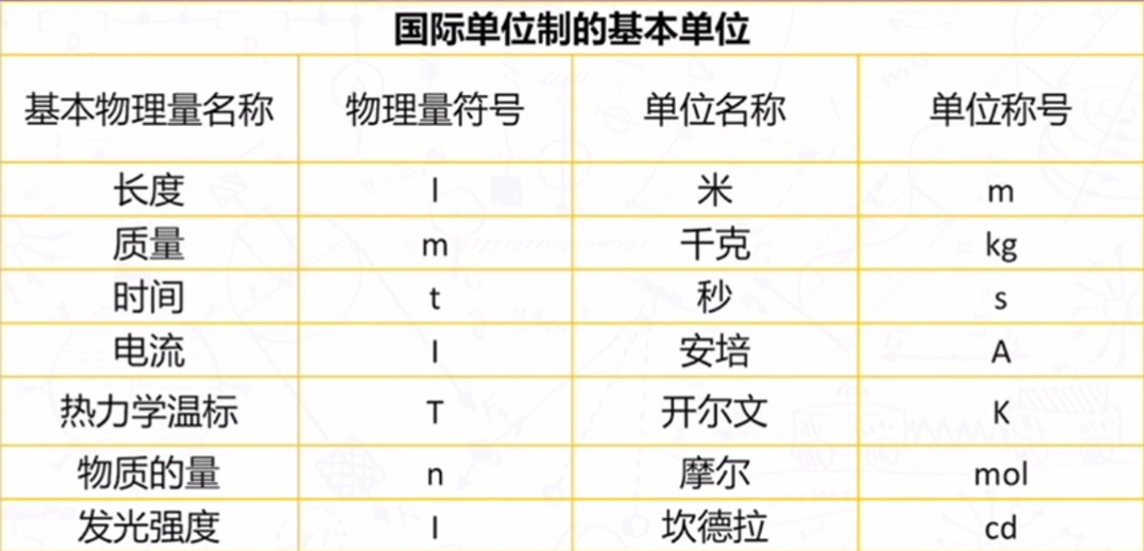
- 基本物理量:只要选定几个物理量,就能够利用物理量之间的关系推导出其他物理量的单位,这些物理量称为基本物理量.
- 基本单位:基本物理量的单位
- 导出单位:用基本单位间通过数学运算得到的单位.
- 单位制:由基本单位和导出单位共同组成. 1960 年第 11 届国际计量大会制定了一种国际通用的,包括一切计算领域的单位制,叫做国际单位制,简称 SI.
- 力的单位是牛顿,用基本单位表达是$1N=1kg \cdot s^2$.
两类问题
轨迹
- 直线:合外力和速度共线
- 曲线:合外力和速度不共线
加速度
- 不变:合外力不变
- 变大:合外力变大
- 变小:合外力变小
速度
- 不变:合外力为 0
- 变大:合外力与速度夹角<$90 ^\circ$
- 变小:合外力与速度夹角>$90 ^\circ$
超重与失重
- 实重:实际所受重力
- 视重:$F_N$
- 超重:视重>实重:a 竖直向上
- 失重:视重<实重:a 竖直向下.当视重=0,完全失重.
牛顿运动定律
连接体
绳、杆、弹簧都可以让物体连接在一起.
根据受力分析运动——轨迹、a、v.
内力公式:$F_内=\frac{m_远}{m_总}\cdot F$是在每个物体所受力的环境相同时有效.
- 绳连接
万能的内力公式:$F_内=\frac{m_远}{m_总}\cdot F$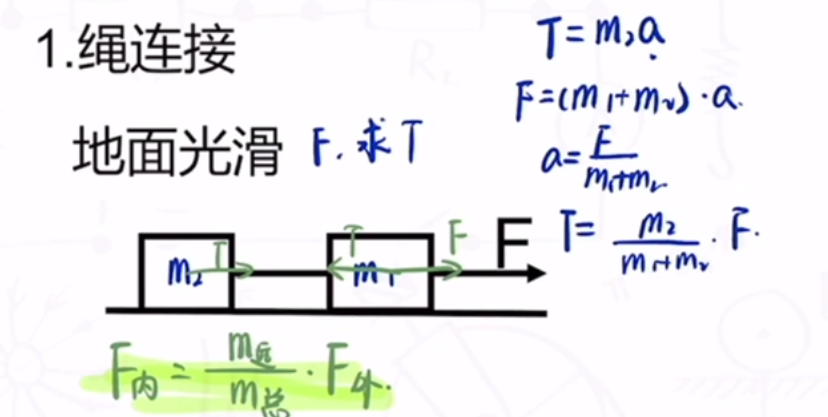
- 弹簧连接
万能的内力公式:$F_内=\frac{m_远}{m_总}\cdot F$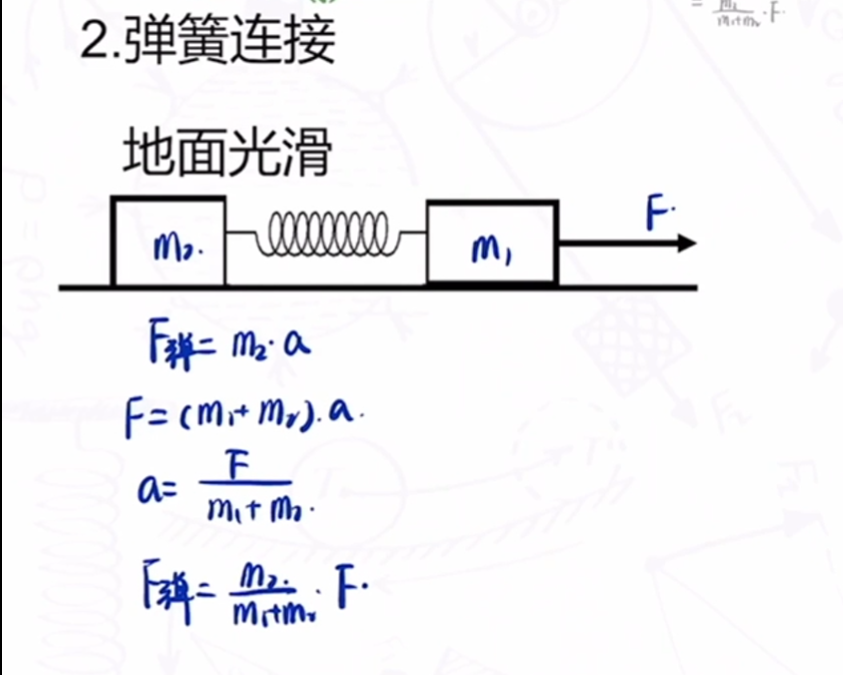
- 挤压连接
万能的内力公式:$F_内=\frac{m_远}{m_总}\cdot F$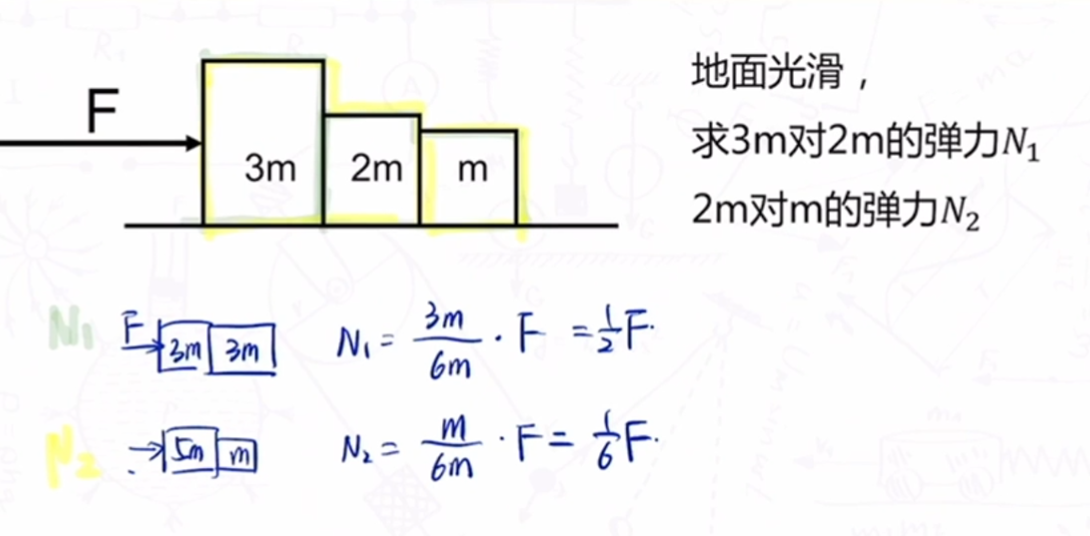
- 摩擦连接
不万能的内力公式:$F_内=\frac{m_远}{m_总}\cdot F$
在地面粗糙的情况下,不符合内力公式!
传送带问题
- 摩擦力方向:使共速

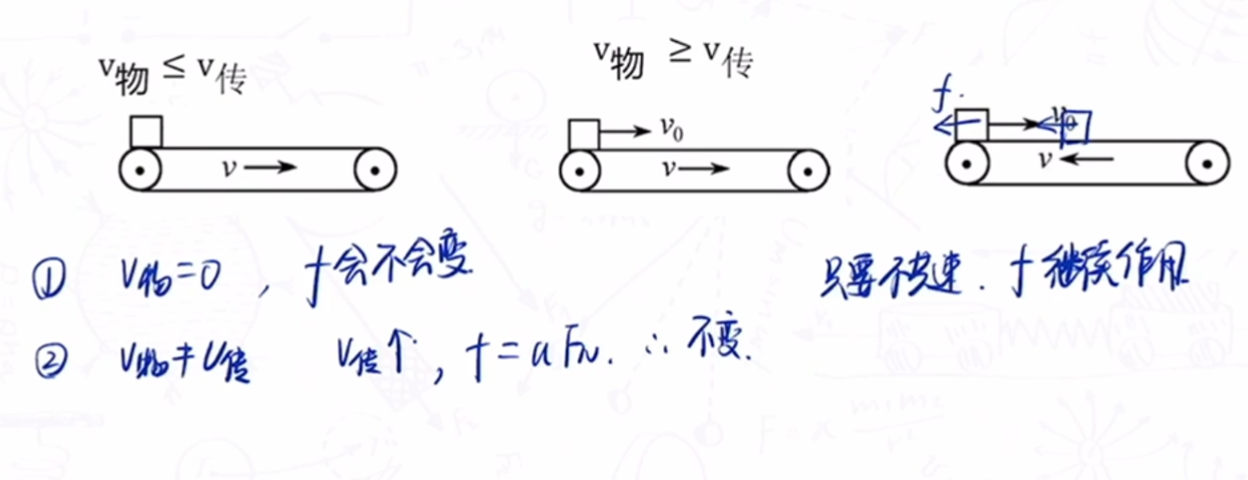
- 共速突变

- v-t 图象

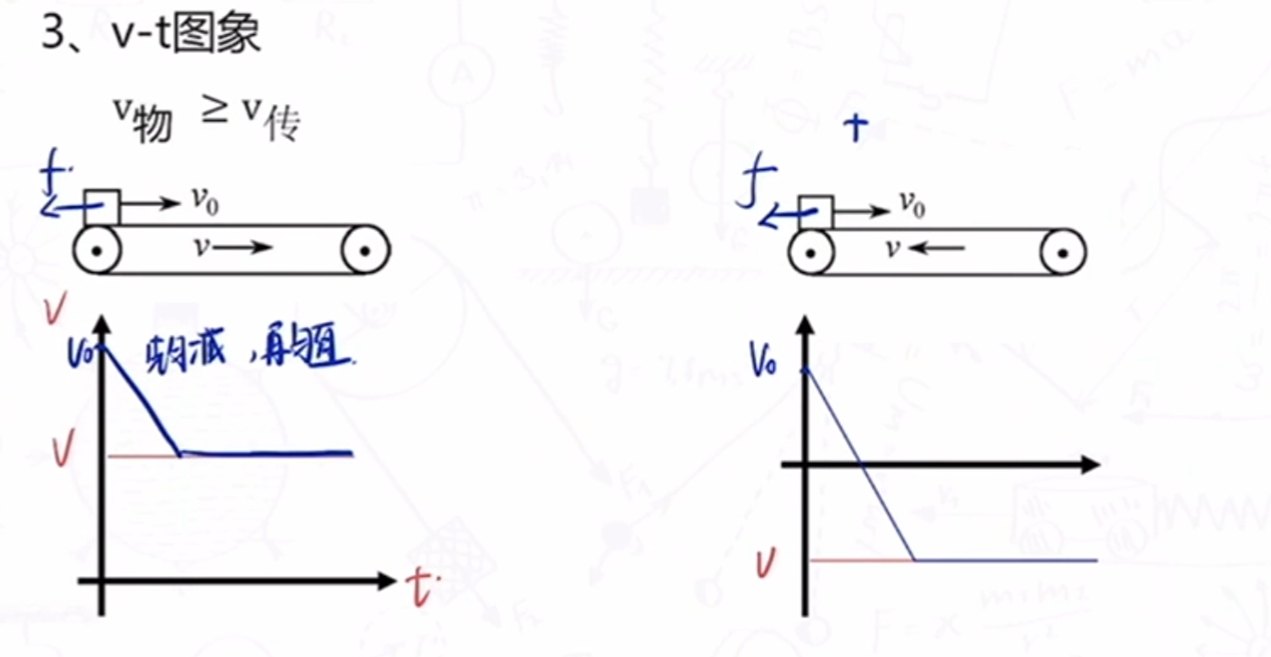
如果传送带上的是小煤块,则痕迹和煤块的距离差就是位移差.
倾斜传送带
共速时重力分力和最大静摩擦的关系,判断运动状态.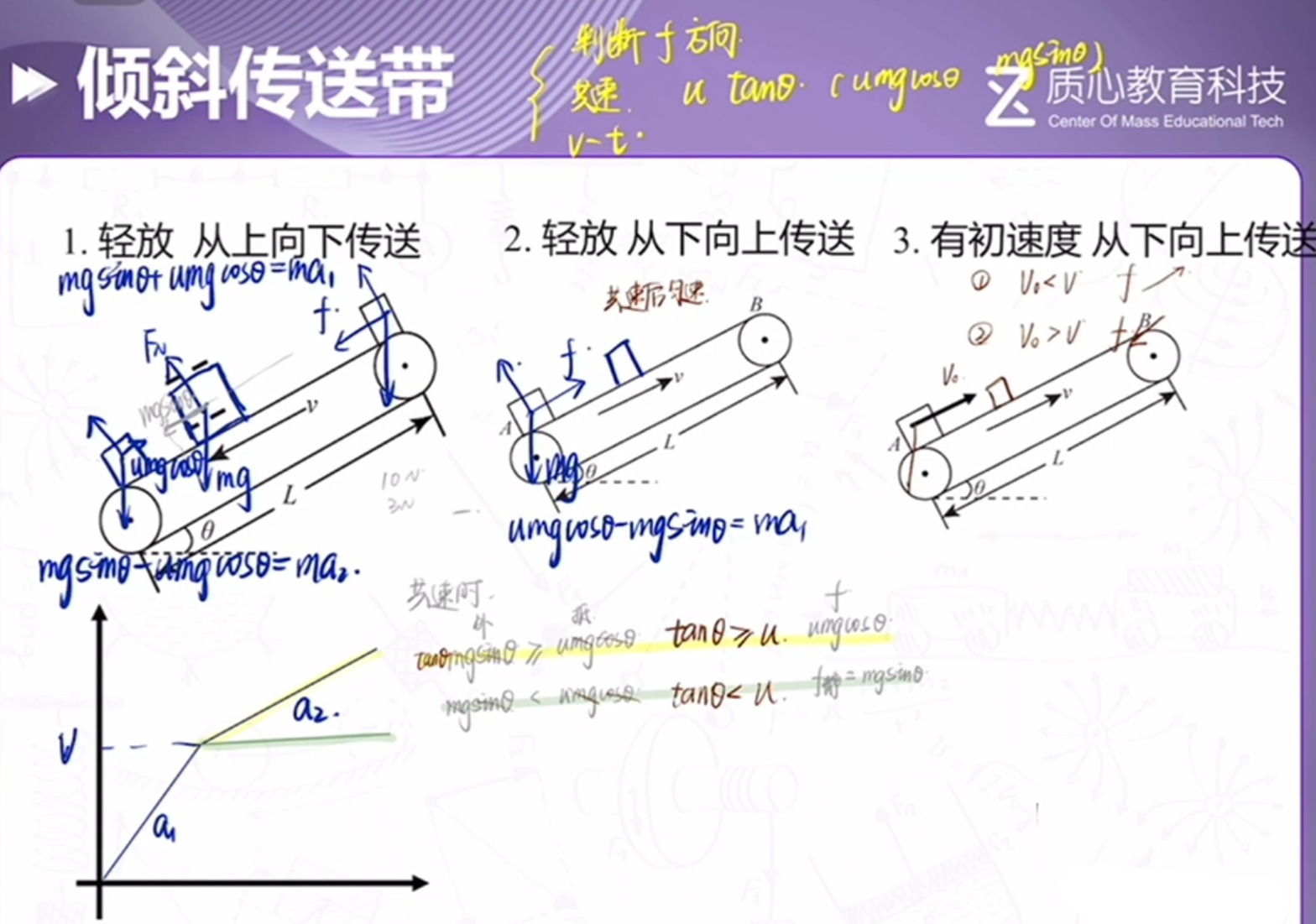
轻放,从上往下传送
- 动因:滑动摩擦力、重力分力
共速后:
- 最大静摩擦力$\ge$重力分力,匀速
- 最大静摩擦力<重力分力,匀加速
轻放,从下往上传送
- 动因:滑动摩擦力
- 共速后:因为滑动摩擦力$\approx$最大静摩擦,而它的动因就是滑动摩擦力,所以静摩擦力=重力分力,匀速
有初速度,从下往上传送
- $v_初>v$,情况 1
- $v_初<v$,情况 2
暂无评论